트라이(Trie)는 문자열에서의 검색을 빠르게 해주는 자료구조입니다.
우리는 정수형 자료형에 대해서 이진검색트리를 이용하면 O(logN)의 시간만에 원하는 데이터를 검색할 수 있습니다.
하지만 문자열에서 이진검색트리를 사용한다면 문자열의 최대 길이가 M이라면 O(MlogN)의 시간 복잡도를 가지게 될 것입니다.
우리는 문자열에서의 검색을 개선하기 위하여 트라이를 이용하여 O(M)의 시간만에 원하는 문자열을 검색할 수 있습니다.
트라이라는 명칭은 Retrieval에서 유래했다고 합니다. 트라이가 retrieve(탐색)하는데 유용한 걸 생각하면 납득이됩니다.
자 그러면 트라이는 어떻게 문자열의 검색을 O(M)만에 처리해 줄 수 있을까요?
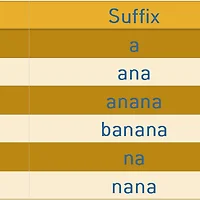
아래 그림은 문자열 집합 = {"AE" , "ATV", "ATES", "ATEV", "DE" ,"DC"} 가 존재할 때 트라이의 예입니다.
쿼리에 따라서 처리해줄 수 있는 역할이 달라지겠지만 우리는 대부분 문자열이 끝나는 지점을 표시하는것이 쿼리를 처리할 때 편합니다.
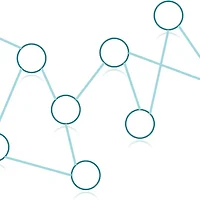
종료 노드들을 표시해주면 위와같은 그림이 되겠군요
자 우리는 트리형태를 띄는 트라이에서 검색을 할 경우 최대 트리의 높이까지 탐색하게 됩니다.
따라서 시간복잡도는 O(H)가 되겠죠 하지만 트리의 높이는 최대 문자열의 길이가 되기 때문에 O(M)의 시간복잡도에 문자열 검색이 가능한 것입니다.
자 그러면 우리는 트라이를 어떻게 구현해야 할까요?
많은 방법이 있겠지만 종만북을 참고하여 가장 보편적인 방법을 보여드리겠습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | struct Trie { bool finish; //끝나는 지점을 표시해줌 Trie* next[26]; //26가지 알파벳에 대한 트라이 Trie() : finish(false) { memset(next, 0, sizeof(next)); } ~Trie() { for (int i = 0; i < 26; i++) if (next[i]) delete next[i]; } void insert(const char* key) { if (*key == '\0') finish = true; //문자열이 끝나는 지점일 경우 표시 else { int curr = *key - 'A'; if (next[curr] == NULL) next[curr] = new Trie(); //탐색이 처음되는 지점일 경우 동적할당 next[curr]->insert(key + 1); //다음 문자 삽입 } } Trie* find(const char* key) { if (*key == '\0')return this;//문자열이 끝나는 위치를 반환 int curr = *key - 'A'; if (next[curr] == NULL)return NULL;//찾는 값이 존재하지 않음 return next[curr]->find(key + 1); //다음 문자를 탐색 } }; | cs |
트라이는 자료구조이기 때문에 입맛에 따라서 변형하여 사용이 가능해야 합니다.
따라서 우리는 문제에서 원하는 조건에 따라서 find함수를 여러방식으로 변형하여 사용하게 될것입니다.
그러면 우리는 트라이를 통하여 어떤 문제를 해결할 수 있을까요??
BOJ 5052 전화번호 목록 문제를 보겠습니다.
전화 번호의 목록이 주어질 때 일관성이 있는지는 확인하는 문제입니다.
우리는 트라이를 이용하여 이 문제를 간단하게 해결할 수 있습니다.
모든 문자열을 트라이에 삽입해준 후 다시 모든 문자열을 트라이로 검색하면서 아직 검색중인데 finish인 부분이 한번이라도 존재한다면 일관성이 없다고 처리가 됩니다.
총 시간 복잡도는 O(T*(N*10))이 되겠군요 여기서 10은 전화번호의 최대길이입니다.
다음은 소스코드입니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | #include <cstdio> #include <algorithm> #include <cstring> #define MAX_N 10000 using namespace std; struct Trie{ Trie* next[10]; bool term; Trie() : term(false){ memset(next,0,sizeof(next)); } ~Trie(){ for(int i=0;i<10;i++){ if(next[i]) delete next[i]; } } void insert(const char* key){ if(*key=='\0') term=true; else{ int curr = *key-'0'; if(next[curr]==NULL) next[curr]=new Trie(); next[curr]->insert(key+1); } } bool find(const char* key){ if(*key=='\0') return 0; if(term) return 1; int curr = *key-'0'; return next[curr]->find(key+1); } }; int t,n,r; char a[MAX_N][11]; int main(){ scanf("%d",&t); while(t--){ scanf("%d",&n); getchar(); for(int i=0;i<n;i++) scanf("%s",&a[i]); Trie *root=new Trie; r=0; for(int i=0;i<n;i++) root->insert(a[i]); for(int i=0;i<n;i++){ if(root->find(a[i])){ r=1; } } printf("%s\n",r?"NO":"YES"); } return 0; } | cs |
자 이제 트라이를 통하여 여러가지 문제들을 풀어봅시다.
'알고리즘 관련 > 알고리즘&이론' 카테고리의 다른 글
| Suffix Array & LCP Array(Longest Common Prefix Array) (4) | 2017.02.08 |
|---|---|
| KMP(Knuth–Morris–Pratt) 알고리즘 (1) | 2017.02.04 |
| 단절점(Articulation Point)와 단절선(Bridge) (1) | 2017.01.31 |
| [최장 증가 수열] LIS(Longest Increasing Subsequence) (33) | 2017.01.25 |
| SCC(Strongly Connected Component) (12) | 2017.01.21 |