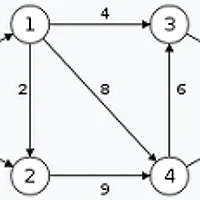
Minimum Path cover in DAG

<Minimum Path cover in DAG>

DAG(Directed Acyclic Graph)에서 모든 정점을 커버하는 겹치지 않는 최소의 경로의 수를 구하는 문제 

전체 정점의 수가 V 커버한 경로상의 간선이 X라면 V-X개의 경로로 커버할 수 있다.

따라서 X를 최대화 시켜야한다. 

간선을 고를 때 제약 조건은 한 정점이 선택 될 때 오직 하나의 indegree와 오직 하나의 outdegree가 선택되어야 한다는 점이다.

즉, indegree와 outdegree가 최대한으로 매칭되어야 한다.  

이를 이용하여 indegree를 상징하는 정점과 outdegree의 정점을 상징하는 정점으로 그래프를 구성하여 해당 그래프의 이분 매칭을 구함으로서 Minimum Path cover in DAG를 구할 수 있다.

참조: http://koosaga.com/entry/Path-Cover-of-DAG