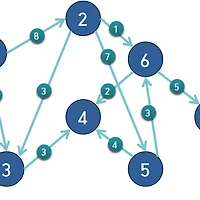
트리에서 임의의 노드 A,B가 있을 때 A와 B의 경로에 C가 존재하는지 여부는 어떻게 알 수 있을까?
A와 B의 LCA를 LCA(A,B)라고 칭해보자.
만약 A와 B의 경로사이에 C가 존재한다면 C는 A와 LCA(A,B) 사이의 경로에 존재하거나 B와 LCA(A,B) 사이의 경로에 존재할 것이다.
일단 A와 LCA(A,B) 사이의 경로에 C가 존재한다고 가정해보자
그렇다면 LCA(A,C)==C && LCA(A,B)==LCA(C,B) 가 성립할 것 이다.
그러면 이번에는 B와 LCA(A,B)사이의 경로에 C가 존재한다고 가정해보자.
그렇다면 LCA(B,C)==C && LCA(A,B)==LCA(C,A) 가 성립할 것이다.
따라서 { LCA(A,C)==C && LCA(A,B)==LCA(C,B) }|| { LCA(B,C)==C && LCA(A,B)==LCA(C,A) } 인 경우 A,B의 경로 사이에 C가 존재한다.
또한 dist(A,C)+dist(C,B)==dist(A,B)의 여부로도 확인 가능하다.
'알고리즘 관련 > 알고리즘&이론' 카테고리의 다른 글
| deque를 이용한 다이나믹프로그래밍 (0) | 2017.09.05 |
|---|---|
| L-R flow (0) | 2017.08.15 |
| 다익스트라 알고리즘(Dijkstra's Algorithm) (7) | 2017.07.09 |
| 트리의 이심률,지름,반지름 (0) | 2017.07.08 |
| (pow(A,B))mod C 를 logB 시간안에 구하는 함수 (0) | 2017.06.18 |