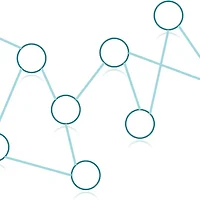
DAG에서 방향성을 거스르지 않게 정점들을 나열하는 알고리즘을 Topological sort(위상 정렬)이라 합니다.
DAG란 Directed Acyclic Graph의 줄임말로 직역하자면 사이클이없는 방향(유향) 그래프 정도가 될 것입니다.
DAG는 유향 그래프에서 정의되며 DAG가 되려면 Cycle이 없어야 합니다.
우리는 유향 그래프에서 한 정점에서 DFS를 실행 할 경우 DFS의 방문순서에 따라서 스패닝 트리를 얻을 수 있습니다.
우리는 이러한 트리를 DFS 스패닝 트리(DFS Spanning Tree)라고 부르며 DFS 스패닝 트리에서 간선의 특징에 따라 간선 분류를 할 수 있습니다.
1. 트리 간선-> 스패닝 트리에 포함된 간선
2. 순방향 간선-> 스패닝 트리에는 포함되지 않았지만 선조에서 자손으로 이어지는 간선
3. 역방향 간선-> 자손에서 선조로 이어지는 간선
4. 교차 간선 -> 위 세 경우가 아닌 간선
위 그림은 최상단 정점에서 DFS를 실행시켰을때의 간선분류상태 입니다.
여기서 역방향 간선에 속하는 간선이 있을 경우 Cycle이 존재하게 되므로 DAG가 아니게 됩니다.
자 우리는 이제 DAG의 정의에 대해 알았으니 위상정렬을 공부할 수 있습니다.
이 글에서는 위상정렬을 구현할 수 있는 두 가지 방법을 소개하려고 합니다.
첫번째로, DFS를 이용하는 방법입니다.
DFS를 실행하면서 DFS가 끝나는 순서대로 기록하면 그 역순이 위상정렬이 됩니다.
쉽게 구현하는 방법은 스택을 이용하여 DFS가 끝나면 스택에 하나씩 삽입해준 후 하나씩 출력해준다면 위상정렬된 상태를 출력할 수 있습니다.
다음과 같은 그래프를 위상 정렬 해보겠습니다.
1번 정점에서 DFS를 실행할 경우 1->2->5->7 순서대로 탐색하고 7번에서 함수 호출이 먼저 종료 될 것입니다. 스택에 함수 호출이 종료되는 순서대로 7 5 2 를 삽입해 준 후 다시 1번 정점으로 돌아옵니다.
다시 1번 정점에서 DFS를 이어나가면 1->3->6 순서대로 탐색하고 6번에서 함수 호출이 먼저 종료 될 것입니다. 스택에 함수 호출이 종료되는 순서대로 6 3 을 삽입해 준 후 다시 1번 정점으로 돌아옵니다.
다시 1번 정점에서 DFS를 이어나가면 4번에서 함수 호출이 종료됩니다. 스택에 4를 삽입해 준후 다시 1번 정점으로 돌아옵니다.
1번 정점에서 더이상 탐색할 정점이 없으므로 스택에 1을 삽입해 줍니다.
자 이제 우리는 스택에서 1 4 3 6 2 5 7 순서대로 꺼낼 수 있습니다.
즉, 1->4->3->6->2->5->7 순서대로 위상 정렬을 한 것입니다.
구현을 보면서 눈치 채신분들도 있으실텐데 위상 정렬은 정확하게 1가지만 나오는게 아닙니다. DFS의 탐색 순서에 따라서 1->3->6->2->5->7->4 와 같은 위상 정렬이 이루어 질 수 도 있습니다.
자 그럼 이번에는 아까의 그래프에서 간선을 딱 하나 추가해보겠습니다.
자 다음과 같이 7번 정점에서 2번 정점으로 향하는 정점하나를 추가했습니다. 위상정렬이 가능할까요?
정답은 불가능합니다.
7에서 2로 향하는 간선은 역방향 간선이기 때문에 2 ->5 ->7 ->2 라는 사이클을 형성하게 됩니다.
그렇다면 우리는 DFS로 위상정렬을 하는 도중에 이러한 사이클을 캐치해낼 수 있을까요?
우리는 DFS를 구현할 때 보통 방문한 정점을 visited 했다고 배열에 표시를 해줍니다. 이 때 visited되있는데 아직 끝나지 않은 정점을 DFS 호출 도중 보게 된다면 현재 보고있는 간선은 역방향 간선이 됩니다.
우리는 finish라는 배열을 따로 생성하여 DFS가 완전히 끝날 때 표시를 해주므로서 역방향 간선 존재 유무를 파악할 수 있습니다.
코드를 구현해 보자면 아래와같이 되겠군요
1 2 3 4 5 6 7 8 9 10 11 | void dfs(int here) { visited[here] = true; for (auto there : vt[here]) { if (!visited[there]) dfs(there); else if (!finish[there]) cycle = 1; } finish[here] = true; st.push(here); } | cs |
이런식으로 DFS가 끝나는 정점을 스택에 넣어줌과 동시에 종료됬다는 표시를 해주면서 사이클 존재 여부를 파악할 수 있습니다.
우리는 DFS를 이용한 위상정렬을 이용해 2252 줄세우기를 풀어볼 수 있습니다.
학생의 키를 비교한 쿼리를 전부 간선으로 생각을 해준 뒤 위상 정렬을 해준 결과를 출력하는 문제입니다.
문제에서 답이 존재하지 않는 경우에 대해 언급을 하지 않았으니 사이클이 존재하지 않는다고 생각해도 될 것 같습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | #include <cstdio> #include <algorithm> #include <vector> #include <stack> #define MAX_N 32000 using namespace std; vector<vector<int>> vt; stack<int> st; int n, m, x, y, visited[MAX_N + 1]; void dfs(int v) { visited[v] = true; for (auto i : vt[v]) { if (visited[i]) continue; dfs(i); } st.push(v); } int main() { scanf("%d%d", &n, &m); vt.resize(n + 1); for (int i = 0; i < m; i++) { scanf("%d%d", &x, &y); vt[x].push_back(y); } for (int i = 1; i <= n; i++) { if (!visited[i]) dfs(i); } while (st.size()) { printf("%d ", st.top()); st.pop(); } return 0; } | cs |
소스 코드는 위와 같이 됩니다.
이제 DFS로 위상 정렬을 하실 수 있겠나요?
자 이번에는 indegree의 수를 이용하는 방법을 설명해 드리겠습니다.
indegree란 한 정점에서 자신에게 들어오는 방향인 간선의 수입니다.
다음과 같은 그래프에서 각정점의 indegree의 개수는
1번 정점: 0
2번 정점: 1
3번 정점: 0
4번 정점: 3
이 됩니다. 즉 화살표 방향이 자기를 향하고 있는 간선의 개수 입니다.
우리는 간선의 정보를 받을 때 모든 정점의 indegree의 개수를 세준 후 queue에 indegree가 0인 정점을 삽입해 줍니다.
정점의 횟수 만큼 반복문을 돌려 다음 작업을 반복합니다.
-> 큐의 front를 추출하여 해당 정점에서 나가는 간선을 다 지워준 후 지워진 간선에 의하여 indegree가 0이 되는 정점들을 queue에 삽입해줍니다. (이때 간선을 지워준 다는 것은 간선의 종점인 정점들의 indegree의 개수를 -1 해줌으로 구현 가능합니다.)
이 때 큐에 동시에 여러개의 원소가 들어간다면 그 정점들의 순서가 바뀌어도 위상 정렬의 결과에는 영향을 주지 않습니다.
하지만 우리가 정점의 횟수만큼 반복문을 돌리던 중 큐의 크기가 먼저 0이 되어 버린다면 사이클이 존재하므로 위상 정렬이 불가능하다는 결론이 나옵니다. 사이클에 속하는 정점들이 존재한다면 그 정점들은 모두 indegree가 1이상이라 큐에 들어가지 않기 때문입니다.
이러한 방식으로 구현하였을 때 큐에서 추출되는 순서대로 위상정렬이 이루어집니다.
다음과 같은 그래프의 위상정렬을 해보겠습니다.
우선 다음과 같이 비어있는 큐를 생성한 뒤 indegree의 개수를 세줍니다.
우선 큐에 indegree가 0인 1번 정점을 삽입해줍니다.
큐의 front인 1번 정점에서 나가는 간선을 모두 지워 준 뒤 indegree가 0이 된 2번 4번 정점을 queue에 삽입합니다.
큐의 front인 2번 정점에서 나가는 간선을 모두 지워 준 뒤 indegree가 0이 된 3번 6번 9번 정점을 queue에 삽입합니다.
큐의 front인 4번 3번 6번 정점에서 나가는 간선을 순서대로 지워준 후 indegree가 0이 된 5번 7번 정점을 queue에 삽입합니다.
큐의 front인 9번 5번 정점에서 나가는 간선을 순서대로 지워준 후 indegree가 0이 된 8번 정점을 queue에 삽입합니다.
큐의 front인 7번 8번 정점에서 나가는 간선을 순서대로 지워 준 후 indegree가 0이 된 10번 11번 정점을 queue에 삽입합니다.
큐의 front인 10번 11번 정점에서 나가는 간선을 순서대로 지워 준 후 indegree가 0이 된 12번 정점을 queue 삽입한 후 12번 정점에서 나가는 간선이 없으니 위상정렬을 종료합니다.
위와같이 위상 정렬을 수행했을 때 1->2->4->3->6->9->5->7->8->10->11->12 의 결과를 얻게 됩니다.
큐에 동시에 여러 원소가 있을 때 그 원소들끼리는 topology에 영향을 주지않는걸 이용하여 BOJ 1766 문제집과 같은 문제를 풀수도 있습니다.
우리는 큐대신 min heap을 이용한다면 동시에 여러 원소가 있을 때 큐는 작은 원소를 먼저 내보낼 것입니다.
이해를 위하여 1766 문제집의 코드를 첨부하겠습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | #include <cstdio> #include <algorithm> #include <vector> #include <queue> #define MAX_N 32000 using namespace std; int n, m, a, b, in[MAX_N + 1]; vector<vector<int>> vt; priority_queue<int> pq; int main() { scanf("%d%d", &n, &m); vt.resize(n + 1); for (int i = 0; i < m; i++) { scanf("%d%d", &a, &b); vt[a].push_back(b); in[b]++; } for (int i = 1; i <= n; i++) { if (!in[i]) pq.push(-i); } while (pq.size()) { int here = -pq.top(); pq.pop(); printf("%d ", here); for (int there : vt[here]) { in[there]--; if (!in[there]) pq.push(-there); } } return 0; } | cs |
자 이제 두가지 방법으로 위상정렬이 가능하신가요?
이제 위상정렬을 이용하여 다양한 문제를 풀어봅시다!
'알고리즘 관련 > 알고리즘&이론' 카테고리의 다른 글
| [자료구조]트라이(Trie) (4) | 2017.02.04 |
|---|---|
| 단절점(Articulation Point)와 단절선(Bridge) (1) | 2017.01.31 |
| [최장 증가 수열] LIS(Longest Increasing Subsequence) (33) | 2017.01.25 |
| SCC(Strongly Connected Component) (12) | 2017.01.21 |
| LCA(Lowest Common Ancestor) (4) | 2017.01.19 |